| GARCH 변동성 추정 - 양적 과학 |
|---|
| 277,487 2024-01-16 |
|
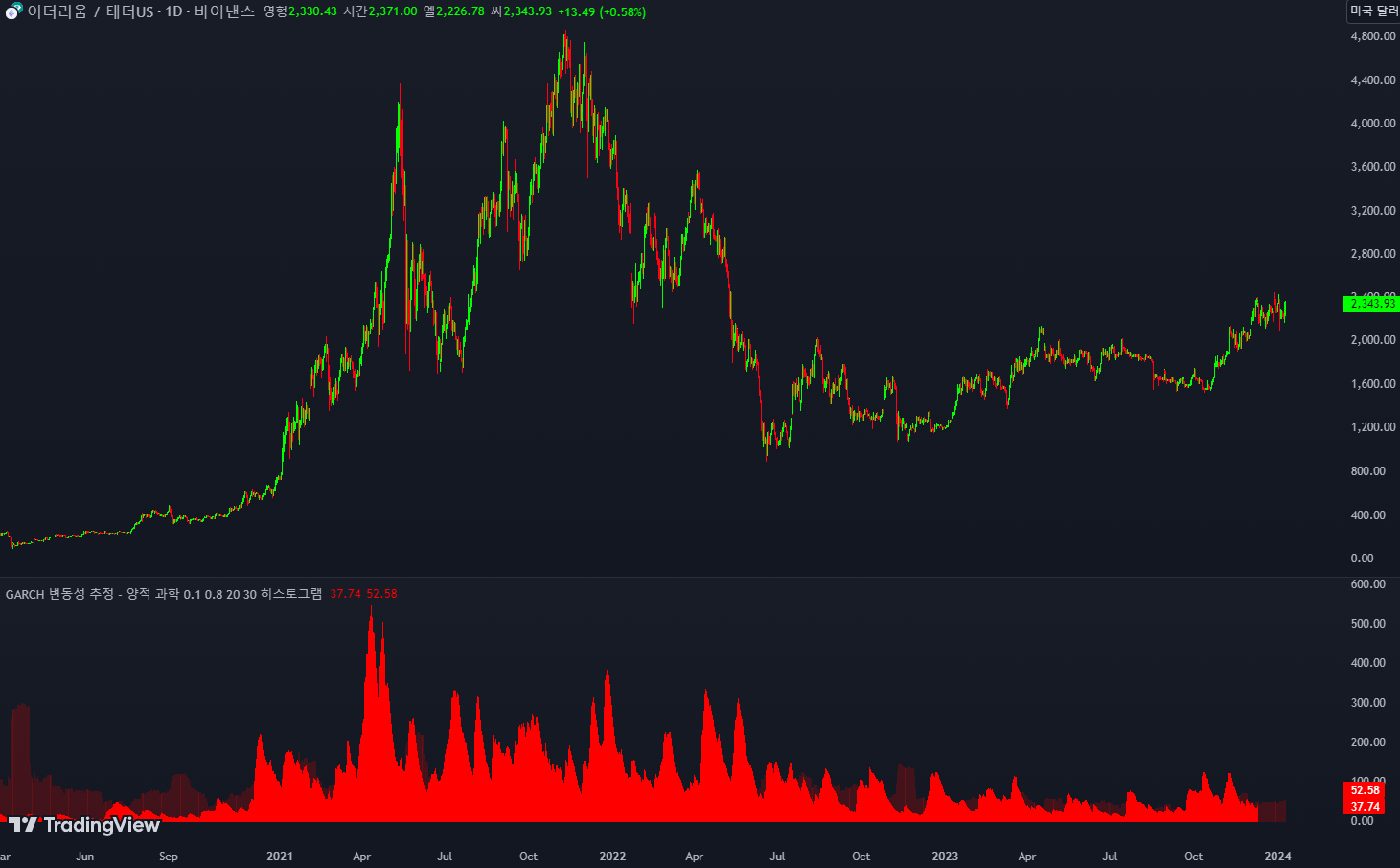
GARCH(Generalized Autoregressive Conditional Heteroskedasticity) 모델은 금융 자산의 변동성을 예측하는 데 사용되는 통계 모델입니다. 이 모델은 시간에 따른 변동성의 변동을 고려하며, 변동성은 이분산적(즉, 일정하지 않은 분산) 방식으로 변할 수 있으며 과거 사건의 영향을 받을 수 있다는 점을 인식합니다.
GARCH 모델의 일반 공식은 다음과 같습니다. σ²(t) = ω + α * ε²(t-1) + β * σ²(t-1) 여기서: σ²(t)는 시간 t에서의 조건부 분산(즉, 제곱 변동성)입니다. ω는 변동성의 기준 수준을 나타내는 상수항(절편) 입니다. α는 조건부 분산에 대한 제곱 지연 오차 항의 영향을 나타내는 계수 입니다. ε²(t-1)은 이전 기간의 제곱 지연 오차 항입니다. β는 현재 조건부 분산에 대한 지연 조건부 분산의 영향을 나타내는 계수입니다 . 재무 예측의 맥락에서 GARCH 모델은 자산의 미래 변동성을 추정하는 데 사용됩니다. 사용 방법 이 양적 지표는 변동성의 가능한 미래 움직임을 추정할 수 있습니다. GARCH가 가치가 상승하면 자산의 변동성도 상승할 가능성이 높으며, 그 반대의 경우도 마찬가지입니다. 이 지표는 GARCH(밝은 빨간색)와 과거 변동성 추세(진한 빨간색)의 관계를 표시합니다. 사용자 인터페이스 알파: 알파의 시작 값을 선택합니다(기본값은 0.10).
베타: 베타의 시작 값을 선택합니다(기본값은 0.80입니다).
길이: EMA(지수 이동 평균) 및 과거 변동성(기본값은 20)과 같은 모델 내 값을 계산하기 위한 기간을 선택합니다.
예측: 예측 기간을 선택하고, 앞으로 데이터를 시각화할 막대 수를 선택합니다(기본 설정은 30입니다).
디자인: 원하는 색상으로 지표를 사용자 지정하고 다양한 유형의 차트에서 선택하여 디자인 설정을 관리합니다.
|
| 이전글 CCI 기반 지원 및 저항 전략 |
| 다음글 캔들 레벨 [프로] |